IPF Performance#
The use of iterative proportional fitting (IPF) is quite common on processes involving doubly-constraining matrices, such as synthetic gravity models and fractional split models (aggregate destination-choice models).
As this is a commonly used algorithm, we have implemented it in Cython, where we can take full advantage of multi-core CPUs. We have also implemented the ability of using both 32-bit and 64-bit floating-point seed matrices, which has direct impact on cache use and consequently computational performance.
In this section, we compare the runtime of AequilibraE’s current implementation of IPF, with a general IPF algorithm written in pure Python, available here.
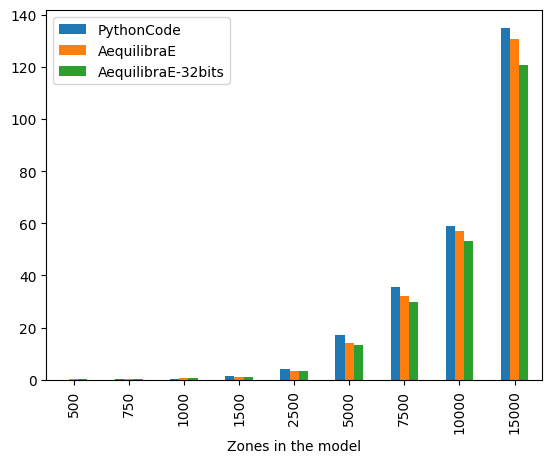
The figure below compares AequilibraE’s IPF runtime with one core with the benchmark Python code. From the figure below, we can notice that the runtimes were practically the same for the instances with 1,000 zones or less. As the number of zones increases, AequilibraE demonstrated to be slightly faster than the benchmark python code, while applying IPF to a 32-bit NumPy array (np.float32) was significantly faster. It’s worth mentioning that the user can set up a threshold for AequilibraE’s IPF function, as well as use more than one core to speed up the fitting process.
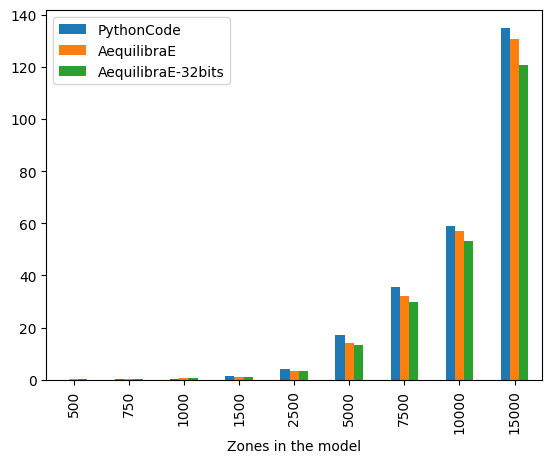
AequilibraE’s IPF runtime#
As IPF is an embarrassingly-parallel workload, it is more relevant to look at the performance of the AequilibraE implementations, starting by comparing the implementation performance for inputs in 32 vs 64 bits using 32 threads.
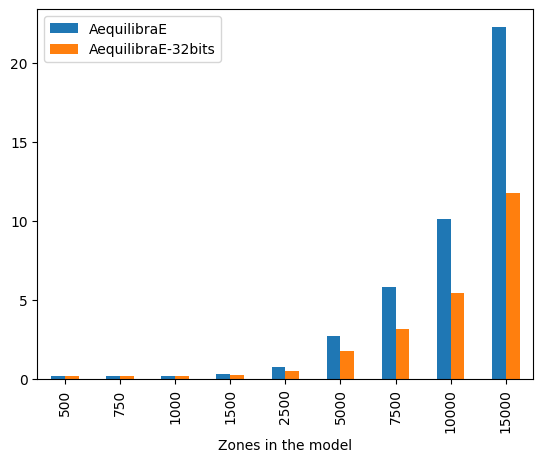
AequilibraE’s IPF runtime 32 vs 64 bits#
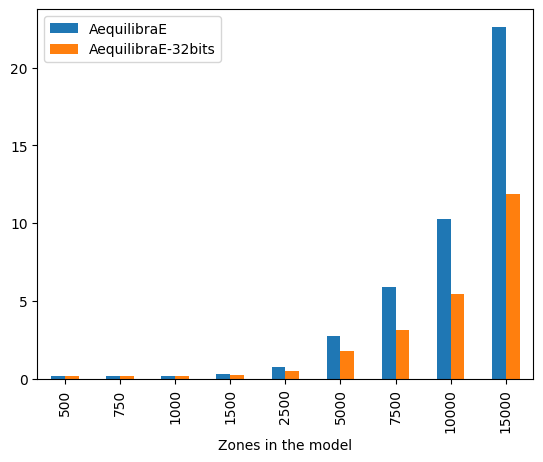
The difference is staggering, with the 32-bit implementation being twice as fast as the 64-bit one for large matrices. It is also worth noting that differences in results between the outputs between these two versions are incredibly small (RMSE < 1.1e-10), and therefore unlikely to be relevant in most applications.
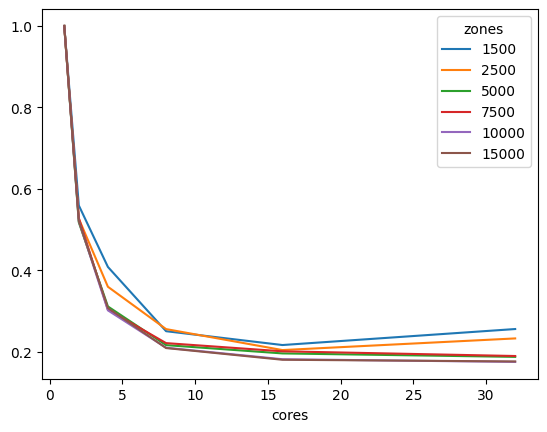
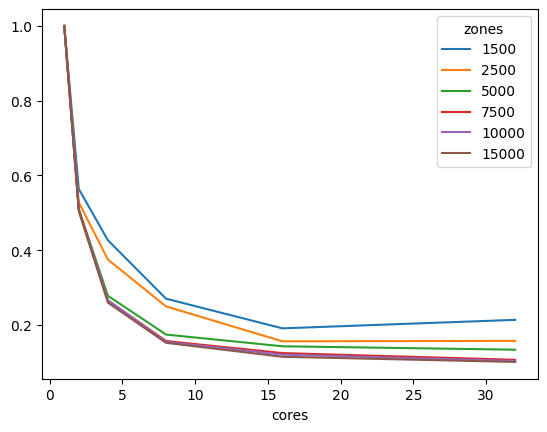
We can also look at performance gain across matrix sizes and number of cores, and it becomes clear that the 32-bit version scales significantly better than its 64-bit counterpart, showing significant performance gains up to 16 threads, while the latter stops showing much improvement beyond 8 threads, likely due to limitations on cache size.
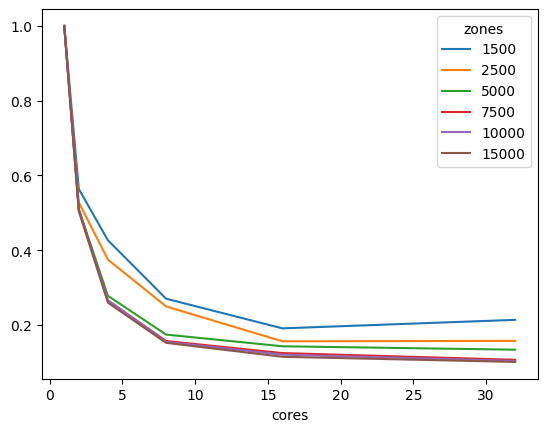
number of cores used in IPF for 64 bit matrices#
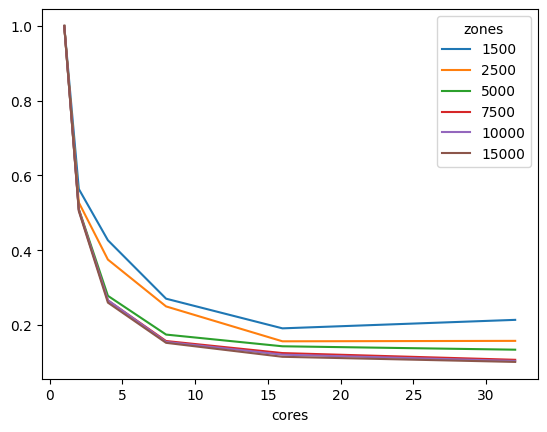
number of cores used in IPF for 32 bit matrices#
In conclusion, AequilibraE’s IPF implementation is over 11 times faster than its pure Python counterpart for large matrices on a workstation, largely due to the use of Cython and multi-threading, but also due to the use of a 32-bit version of the algorithm.
These tests were run on a Threadripper 3970x (released in 2019) workstation with 32 cores (64 threads) @ 3.7 GHz and 256 Gb of RAM. The code is provided below for reference.
Reference code#
from copy import deepcopy
from time import perf_counter
import numpy as np
import pandas as pd
from aequilibrae.distribution.ipf_core import ipf_core
from tqdm import tqdm
# From:
# https://github.com/joshchea/python-tdm/blob/master/scripts/CalcDistribution.py
def CalcFratar(ProdA, AttrA, Trips1, maxIter=10):
'''Calculates fratar trip distribution
ProdA = Production target as array
AttrA = Attraction target as array
Trips1 = Seed trip table for fratar
maxIter (optional) = maximum iterations, default is 10
Returns fratared trip table
'''
# print('Checking production, attraction balancing:')
sumP = ProdA.sum()
sumA = AttrA.sum()
# print('Production: ', sumP)
# print('Attraction: ', sumA)
if sumP != sumA:
# print('Productions and attractions do not balance, attractions will be scaled to productions!')
AttrA = AttrA*(sumP/sumA)
else:
pass
# print('Production, attraction balancing OK.')
# Run 2D balancing --->
for balIter in range(0, maxIter):
ComputedProductions = Trips1.sum(1)
ComputedProductions[ComputedProductions == 0] = 1
OrigFac = (ProdA/ComputedProductions)
Trips1 = Trips1*OrigFac[:, np.newaxis]
ComputedAttractions = Trips1.sum(0)
ComputedAttractions[ComputedAttractions == 0] = 1
DestFac = (AttrA/ComputedAttractions)
Trips1 = Trips1*DestFac
return Trips1
mat_sizes = [500, 750, 1000, 1500, 2500, 5000, 7500, 10000, 15000]
#Benchmarking
bench_data = []
cores = 1
repetitions = 5
iterations = 100
for zones in mat_sizes:
for repeat in tqdm(range(repetitions), f"Repetitions for zone size {zones}"):
mat1 = np.random.rand(zones, zones)
target_prod = np.random.rand(zones)
target_atra = np.random.rand(zones)
target_atra *= target_prod.sum()/target_atra.sum()
aeq_mat = deepcopy(mat1)
# We use a nonsensical negative tolerance to force it to run all iterations
# and set warning for non-convergence to false, as we know it won't converge
t = perf_counter()
ipf_core(aeq_mat, target_prod, target_atra, max_iterations=iterations, tolerance=-5, cores=cores, warn=False)
aeqt = perf_counter() - t
aeq_mat32 = np.array(mat1, np.float32)
# We now run the same thing with a seed matrix in single-precision (float 32 bits) instead of double as above (64 bits)
t = perf_counter()
ipf_core(aeq_mat32, target_prod, target_atra, max_iterations=iterations, tolerance=-5, cores=cores, warn=False)
aeqt2 = perf_counter() - t
bc_mat = deepcopy(mat1)
t = perf_counter()
x = CalcFratar(target_prod, target_atra, bc_mat, maxIter=iterations)
bench_data.append([zones, perf_counter() - t, aeqt, aeqt2])
Repetitions for zone size 500: 100%|██████████| 5/5 [00:01<00:00, 2.60it/s]
Repetitions for zone size 750: 100%|██████████| 5/5 [00:04<00:00, 1.18it/s]
Repetitions for zone size 1000: 100%|██████████| 5/5 [00:07<00:00, 1.57s/it]
Repetitions for zone size 1500: 100%|██████████| 5/5 [00:19<00:00, 3.88s/it]
Repetitions for zone size 2500: 100%|██████████| 5/5 [00:56<00:00, 11.24s/it]
Repetitions for zone size 5000: 100%|██████████| 5/5 [03:44<00:00, 44.89s/it]
Repetitions for zone size 7500: 100%|██████████| 5/5 [08:09<00:00, 97.89s/it]
Repetitions for zone size 10000: 100%|██████████| 5/5 [14:11<00:00, 170.34s/it]
Repetitions for zone size 15000: 100%|██████████| 5/5 [32:23<00:00, 388.70s/it]
bench_df = pd.DataFrame(bench_data, columns=["Zones in the model", "PythonCode", "AequilibraE", "AequilibraE-32bits"])
bench_df.groupby(["Zones in the model"]).mean().plot.bar()
<Axes: xlabel='Zones in the model'>
bench_df.groupby(["Zones in the model"]).mean()
| PythonCode | AequilibraE | AequilibraE-32bits | |
|---|---|---|---|
| Zones in the model | |||
| 500 | 0.103166 | 0.140051 | 0.137266 |
| 750 | 0.241757 | 0.302931 | 0.297389 |
| 1000 | 0.513984 | 0.529727 | 0.516339 |
| 1500 | 1.416848 | 1.276844 | 1.156637 |
| 2500 | 4.253563 | 3.581645 | 3.333664 |
| 5000 | 17.059166 | 14.288760 | 13.257936 |
| 7500 | 35.568686 | 32.021563 | 29.666000 |
| 10000 | 59.030967 | 57.028204 | 53.155270 |
| 15000 | 134.895915 | 130.652199 | 120.535656 |
#Benchmarking 32 threads
bench_data_parallel = []
cores = 32
repetitions = 5
iterations = 100
for zones in mat_sizes:
for repeat in tqdm(range(repetitions), f"Repetitions for zone size {zones}"):
mat1 = np.random.rand(zones, zones)
target_prod = np.random.rand(zones)
target_atra = np.random.rand(zones)
target_atra *= target_prod.sum()/target_atra.sum()
aeq_mat = deepcopy(mat1)
# We use a nonsensical negative tolerance to force it to run all iterations
# and set warning for non-convergence to false, as we know it won't converge
t = perf_counter()
ipf_core(aeq_mat, target_prod, target_atra, max_iterations=iterations, tolerance=-5, cores=cores, warn=False)
aeqt = perf_counter() - t
aeq_mat32 = np.array(mat1, np.float32)
# We now run the same thing with a seed matrix in single-precision (float 32 bits) instead of double as above (64 bits)
t = perf_counter()
ipf_core(aeq_mat32, target_prod, target_atra, max_iterations=iterations, tolerance=-5, cores=cores, warn=False)
aeqt2 = perf_counter() - t
rmse = np.sqrt(np.mean((aeq_mat-aeq_mat32)**2))
bench_data_parallel.append([zones, aeqt, aeqt2, rmse])
Repetitions for zone size 500: 100%|██████████| 5/5 [00:01<00:00, 2.70it/s]
Repetitions for zone size 750: 100%|██████████| 5/5 [00:01<00:00, 2.64it/s]
Repetitions for zone size 1000: 100%|██████████| 5/5 [00:02<00:00, 2.37it/s]
Repetitions for zone size 1500: 100%|██████████| 5/5 [00:03<00:00, 1.61it/s]
Repetitions for zone size 2500: 100%|██████████| 5/5 [00:07<00:00, 1.41s/it]
Repetitions for zone size 5000: 100%|██████████| 5/5 [00:24<00:00, 4.91s/it]
Repetitions for zone size 7500: 100%|██████████| 5/5 [00:49<00:00, 9.96s/it]
Repetitions for zone size 10000: 100%|██████████| 5/5 [01:26<00:00, 17.29s/it]
Repetitions for zone size 15000: 100%|██████████| 5/5 [03:10<00:00, 38.02s/it]
bench_df_parallel = pd.DataFrame(bench_data_parallel, columns=["Zones in the model", "AequilibraE", "AequilibraE-32bits", "rmse"])
bench_df_parallel.groupby(["Zones in the model"]).mean()[[ "AequilibraE", "AequilibraE-32bits"]].plot.bar()
<Axes: xlabel='Zones in the model'>
bench_df_parallel.groupby(["Zones in the model"]).mean()
| AequilibraE | AequilibraE-32bits | rmse | |
|---|---|---|---|
| Zones in the model | |||
| 500 | 0.170232 | 0.172460 | 1.080659e-10 |
| 750 | 0.183474 | 0.183857 | 7.100473e-11 |
| 1000 | 0.211237 | 0.191961 | 5.137420e-11 |
| 1500 | 0.322709 | 0.252115 | 3.358886e-11 |
| 2500 | 0.779715 | 0.522037 | 2.036197e-11 |
| 5000 | 2.745004 | 1.760100 | 9.588117e-12 |
| 7500 | 5.900431 | 3.170006 | 6.258958e-12 |
| 10000 | 10.255305 | 5.456631 | 4.733115e-12 |
| 15000 | 22.618665 | 11.860497 | 3.102268e-12 |
cores_to_use = [1, 2, 4, 8, 16, 32]
aeq_data = []
repetitions = 1
iterations = 50
for zones in mat_sizes:
for cores in tqdm(cores_to_use,f"Zone size: {zones}"):
for repeat in range(repetitions):
mat1 = np.random.rand(zones, zones)
target_prod = np.random.rand(zones)
target_atra = np.random.rand(zones)
target_atra *= target_prod.sum()/target_atra.sum()
aeq_mat = np.array(deepcopy(mat1), np.float32)
t = perf_counter()
ipf_core(aeq_mat, target_prod, target_atra, max_iterations=iterations, tolerance=-5, cores=cores, warn=False)
aeqt = perf_counter() - t
aeq_data.append([zones, cores, aeqt])
Zone size: 500: 100%|██████████| 6/6 [00:00<00:00, 12.14it/s]
Zone size: 750: 100%|██████████| 6/6 [00:00<00:00, 10.20it/s]
Zone size: 1000: 100%|██████████| 6/6 [00:00<00:00, 6.87it/s]
Zone size: 1500: 100%|██████████| 6/6 [00:01<00:00, 3.42it/s]
Zone size: 2500: 100%|██████████| 6/6 [00:04<00:00, 1.32it/s]
Zone size: 5000: 100%|██████████| 6/6 [00:16<00:00, 2.73s/it]
Zone size: 7500: 100%|██████████| 6/6 [00:35<00:00, 5.93s/it]
Zone size: 10000: 100%|██████████| 6/6 [01:02<00:00, 10.46s/it]
Zone size: 15000: 100%|██████████| 6/6 [02:21<00:00, 23.62s/it]
aeq_df = pd.DataFrame(aeq_data, columns=["zones", "cores", "time"])
aeq_df = aeq_df[aeq_df.zones>1000]
aeq_df = aeq_df.groupby(["zones", "cores"]).mean().reset_index()
aeq_df = aeq_df.pivot_table(index="zones", columns="cores", values="time")
for cores in cores_to_use[::-1]:
aeq_df.loc[:, cores] /= aeq_df[1]
aeq_df.transpose().plot()
aeq_df
| cores | 1 | 2 | 4 | 8 | 16 | 32 |
|---|---|---|---|---|---|---|
| zones | ||||||
| 1500 | 1.0 | 0.563866 | 0.426711 | 0.270452 | 0.191147 | 0.213856 |
| 2500 | 1.0 | 0.527781 | 0.375033 | 0.249776 | 0.156473 | 0.157657 |
| 5000 | 1.0 | 0.510183 | 0.278150 | 0.174469 | 0.143175 | 0.134064 |
| 7500 | 1.0 | 0.508706 | 0.265835 | 0.157217 | 0.125007 | 0.107014 |
| 10000 | 1.0 | 0.507172 | 0.266192 | 0.154844 | 0.120771 | 0.103968 |
| 15000 | 1.0 | 0.504696 | 0.259933 | 0.152394 | 0.115052 | 0.101344 |
aeq_data = []
repetitions = 1
iterations = 50
for zones in mat_sizes:
for cores in tqdm(cores_to_use,f"Zone size: {zones}"):
for repeat in range(repetitions):
mat1 = np.random.rand(zones, zones)
target_prod = np.random.rand(zones)
target_atra = np.random.rand(zones)
target_atra *= target_prod.sum()/target_atra.sum()
aeq_mat = np.array(deepcopy(mat1), np.float64)
t = perf_counter()
ipf_core(aeq_mat, target_prod, target_atra, max_iterations=iterations, tolerance=-5, cores=cores, warn=False)
aeqt = perf_counter() - t
aeq_data.append([zones, cores, aeqt])
Zone size: 500: 100%|██████████| 6/6 [00:00<00:00, 12.51it/s]
Zone size: 750: 100%|██████████| 6/6 [00:00<00:00, 9.19it/s]
Zone size: 1000: 100%|██████████| 6/6 [00:00<00:00, 6.50it/s]
Zone size: 1500: 100%|██████████| 6/6 [00:01<00:00, 3.07it/s]
Zone size: 2500: 100%|██████████| 6/6 [00:05<00:00, 1.17it/s]
Zone size: 5000: 100%|██████████| 6/6 [00:18<00:00, 3.14s/it]
Zone size: 7500: 100%|██████████| 6/6 [00:42<00:00, 7.10s/it]
Zone size: 10000: 100%|██████████| 6/6 [01:15<00:00, 12.51s/it]
Zone size: 15000: 100%|██████████| 6/6 [02:47<00:00, 27.93s/it]
aeq_df = pd.DataFrame(aeq_data, columns=["zones", "cores", "time"])
aeq_df = aeq_df[aeq_df.zones>1000]
aeq_df = aeq_df.groupby(["zones", "cores"]).mean().reset_index()
aeq_df = aeq_df.pivot_table(index="zones", columns="cores", values="time")
for cores in cores_to_use[::-1]:
aeq_df.loc[:, cores] /= aeq_df[1]
aeq_df.transpose().plot()
aeq_df
| cores | 1 | 2 | 4 | 8 | 16 | 32 |
|---|---|---|---|---|---|---|
| zones | ||||||
| 1500 | 1.0 | 0.559114 | 0.408111 | 0.250297 | 0.216308 | 0.255603 |
| 2500 | 1.0 | 0.526490 | 0.359411 | 0.255447 | 0.203943 | 0.232535 |
| 5000 | 1.0 | 0.517601 | 0.311059 | 0.216065 | 0.195720 | 0.187223 |
| 7500 | 1.0 | 0.528070 | 0.303304 | 0.221032 | 0.200886 | 0.189343 |
| 10000 | 1.0 | 0.520901 | 0.301453 | 0.209669 | 0.181450 | 0.174836 |
| 15000 | 1.0 | 0.520769 | 0.307402 | 0.208882 | 0.180139 | 0.176024 |