Hyperpath routing#
Hyperpath routing is one of the basic concepts in transit assignment models, and it is a way of representing the set of optimal routes that a passenger can take from an origin to a destination, based on some criterion such as travel time or generalized cost. A hyperpath is a collection of links that form a subgraph of the transit network. Each link in the hyperpath also has a probability of being used by the passenger, which reflects the attractiveness and uncertainty of the route choice. The shortest hyperpath is optimal regarding the combination of paths weighted by the probability of being used.
Hyperpath routing can be applied to different types of transit assignment models, but here we will focus on frequency-based models. Frequency-based models assume that passengers do not have reliable information about the service schedules and arrival times, and they choose their routes based on the expected travel time or cost. This type of model is suitable for transit systems with rather frequent services.
To illustrate how hyperpath routing works in frequency-based models, we will use the algorithm by Spiess and Florian [1] implemented in AequilibraE.
For example purposes, we will use a simple grid network as an Python example to demonstrate how a hyperpath depends on link frequency for a given origin-destination pair. Note that it can be extended to other contexts such as risk-averse vehicle navigation [2].
Bell’s network#
We start by defining the directed graph \(\mathcal{G} = \left( V, E \right)\), where \(V\) and \(E\) are the graph vertices and edges. The hyperpath generating algorithm requires 2 attributes for each edge \(a \in V\):
edge travel time: \(u_a \geq 0\)
edge frequency: \(f_a \geq 0\)
The edge frequency is inversely related to the exposure to delay. For example, in a transit network, a boarding edge has a frequency that is the inverse of the headway (or half the headway, depending on the model assumptions). A walking edge has no exposure to delay, so its frequency is assumed to be infinite.
Bell’s network is a synthetic network: it is a \(n\)-by-\(n\) grid bi-directional network [2] [3]. The edge travel time is taken as random number following a uniform distribution:
To demonstrate how the hyperpath depends on the exposure to delay, we will use a positive constant (\(\alpha\)) and a base delay (\(d_a\)) for each edge that follows a uniform distribution:
The constant \(\alpha \geq 0\) allows us to adjust the edge frequency as follows:
Notice that a smaller \(\alpha\) value implies higher edge frequencies, and vice versa.
Hyperpath computation#
Let’s create a function that:
creates the network,
computes the edge frequency given an input value for \(\alpha\),
computes the shortest hyperpath,
and plots the network and hyperpath.
We start with \(\alpha=0\). This implies that there is no delay over all the network. The
resulting hyperpath corresponds to the same shortest path that Dijkstra’s algorithm would have
computed. You can call NetworkX’s method nx.dijkstra_path to compute the shortest path.
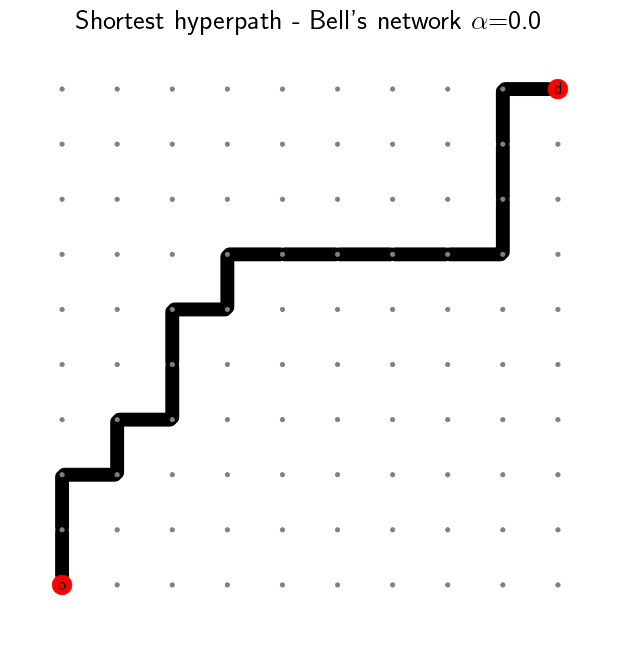
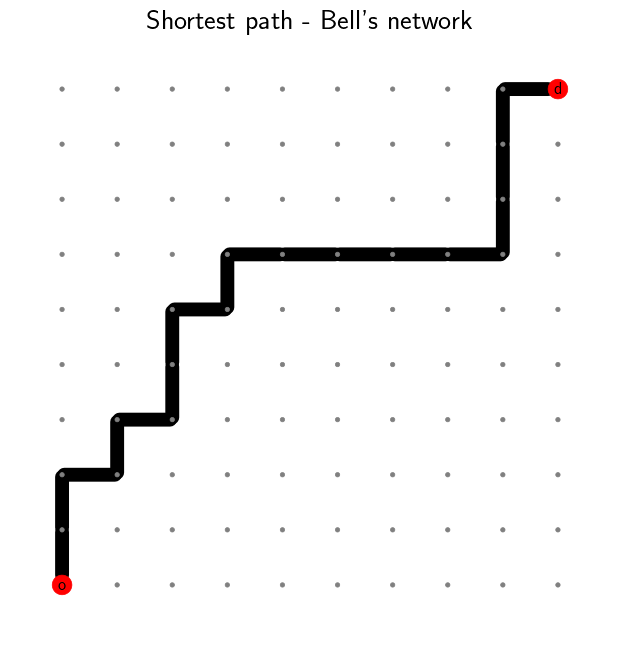
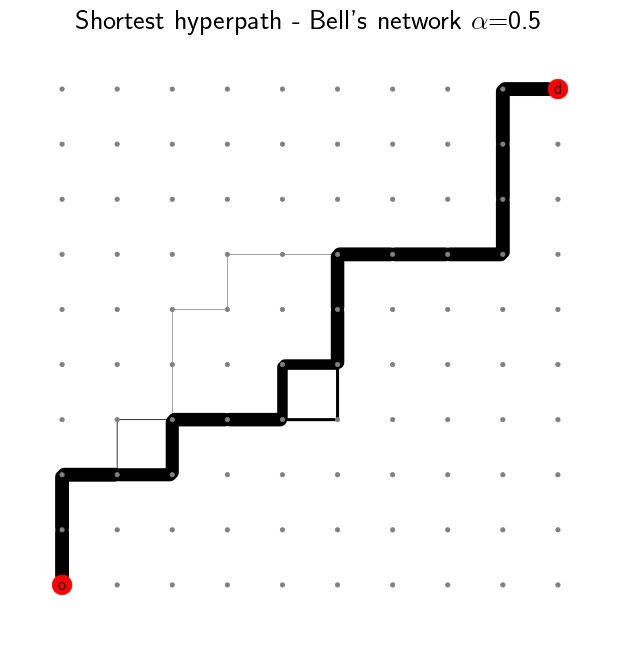
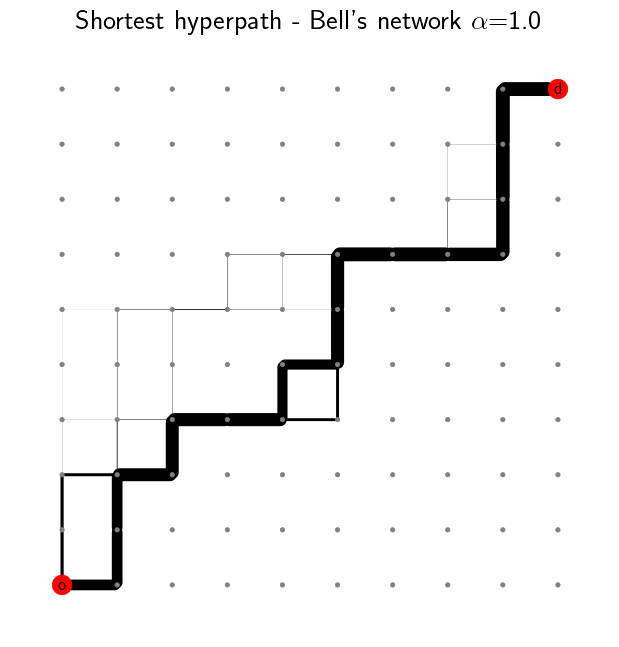
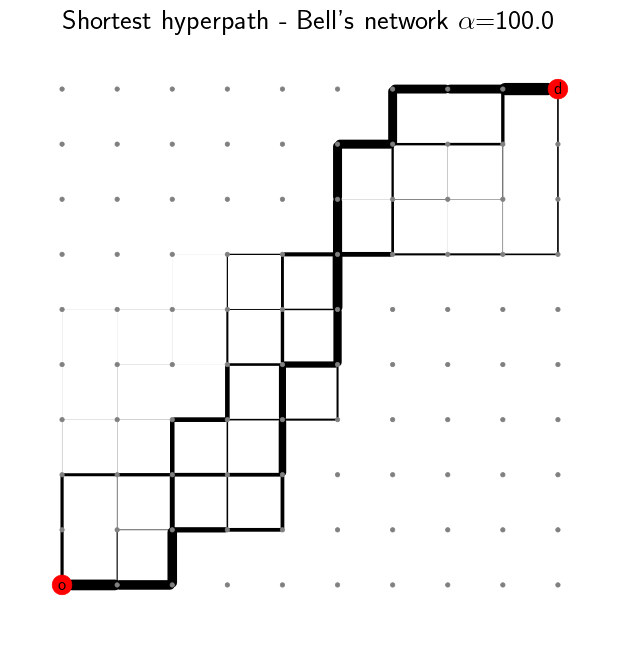
To introduce some delay in the network, we can increase the value of \(\alpha\). We notice that the shortest path is no longer unique and multiple routes are suggested. The link usage probability is reflected by the line width. The majority of the flow still follows the shortest path, but some of it is distributed among different alternative paths. This becomes more apparent as we further increase \(\alpha\).
The code below allows you to reproduce the same experiment that resulted in the previous figures.
# Let's import some packages
import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
import pandas as pd
from aequilibrae.paths.public_transport import HyperpathGenerating
from numba import jit
RANDOM_SEED = 124 # random seed
FIGURE_SIZE = (6, 6) # figure size
def create_vertices(n):
x = np.linspace(0, 1, n)
y = np.linspace(0, 1, n)
xv, yv = np.meshgrid(x, y, indexing="xy")
vertices = pd.DataFrame()
vertices["x"] = xv.ravel()
vertices["y"] = yv.ravel()
return vertices
@jit
def create_edges_numba(n):
m = 2 * n * (n - 1)
tail = np.zeros(m, dtype=np.uint32)
head = np.zeros(m, dtype=np.uint32)
k = 0
for i in range(n - 1):
for j in range(n):
tail[k] = i + j * n
head[k] = i + 1 + j * n
k += 1
tail[k] = j + i * n
head[k] = j + (i + 1) * n
k += 1
return tail, head
def create_edges(n, seed=124):
tail, head = create_edges_numba(n)
edges = pd.DataFrame()
edges["tail"] = tail
edges["head"] = head
m = len(edges)
rng = np.random.default_rng(seed=seed)
edges["trav_time"] = rng.uniform(0.0, 1.0, m)
edges["delay_base"] = rng.uniform(0.0, 1.0, m)
return edges
def generate_hyperpath(n, alpha):
edges = create_edges(n, seed=RANDOM_SEED)
delay_base = edges.delay_base.values
indices = np.where(delay_base == 0.0)
delay_base[indices] = 1.0
freq_base = 1.0 / delay_base
freq_base[indices] = np.inf
edges["freq_base"] = freq_base
if alpha == 0.0:
edges["freq"] = np.inf
else:
edges["freq"] = edges.freq_base / alpha
# Spiess & Florian
sf = HyperpathGenerating(
edges, tail="tail", head="head", trav_time="trav_time", freq="freq"
)
sf.run(origin=0, destination=n * n - 1, volume=1.0)
return sf
def plot_shortest_hyperpath(n=10, alpha=10.0, is_dijkstra=False, figsize=FIGURE_SIZE, title=""):
vertices = create_vertices(n)
n_vertices = n * n
sf = generate_hyperpath(n, alpha)
attr = "trav_time" if is_dijkstra else "volume"
# NetworkX
G = nx.from_pandas_edgelist(
sf._edges,
source="tail",
target="head",
edge_attr=attr,
create_using=nx.DiGraph,
)
if is_dijkstra:
nodes = nx.dijkstra_path(G, 0, n*n-1, weight='trav_time')
edges = list(nx.utils.pairwise(nodes))
widths = 1e2 * np.array([1 if (u,v) in edges else 0 for u, v in G.edges()]) / n
else:
widths = 1e2 * np.array([G[u][v]["volume"] for u, v in G.edges()]) / n
pos = vertices[["x", "y"]].values
_ = plt.figure(figsize=figsize)
node_colors = n_vertices * ["gray"]
node_colors[0] = "r"
node_colors[-1] = "r"
ns = 100 / n
node_size = n_vertices * [ns]
node_size[0] = 20 * ns
node_size[-1] = 20 * ns
labeldict = {}
labeldict[0] = "O"
labeldict[n * n - 1] = "D"
nx.draw(
G,
pos=pos,
width=widths,
node_size=node_size,
node_color=node_colors,
arrowstyle="-",
labels=labeldict,
with_labels=True,
)
ax = plt.gca()
_ = ax.set_title(title, color="k")
plot_shortest_hyperpath(n=10, alpha=0.0, title="Shortest hyperpath - Bell's Network $\\alpha$=0.0")
plot_shortest_hyperpath(n=10, alpha=0.0, is_dijkstra=True, title="Shortest path - Dijkstra's Algorithm")
plot_shortest_hyperpath(n=10, alpha=0.5, title="Shortest hyperpath - Bell's Network $\\alpha$=0.5")
plot_shortest_hyperpath(n=10, alpha=1.0, title="Shortest hyperpath - Bell's Network $\\alpha$=1.0")
plot_shortest_hyperpath(n=10, alpha=100.0, title="Shortest hyperpath - Bell's Network $\\alpha$=100.0")