Transit assignment graph#

In this section, we describe a graph structure for a transit network used for static, link-based, frequency-based assignment. Our focus is the classic algorithm optimal strategies by Spiess and Florian (1989) [1].

Let’s start by giving a few definitions:

  • transit: according to Wikipedia, it is a “system of transport for passengers by group travel systems available for use by the general public unlike private transport, typically managed on a schedule, operated on established routes, and that charge a posted fee for each trip.”

  • transit network: a set of transit lines and stops, where passengers can board, alight or change vehicles.

  • assignment: distribution of the passengers (demand) on the network (supply), knowing that transit users attempt to minimize total travel time, time or distance walking, time waiting, number of transfers, fares, etc…

  • static assignment: assignment without time evolution. Dynamic properties of the flows, such as congestion, are not well described, unlike with dynamic assignment models.

  • schedule-based approach: in this approach, distinct vehicle trips are represented by distinct links. We can see the associated network as a time-expanded network, where the third dimension would be time.

  • frequency-based (or headway-based) approach: unlike with the schedule-based approach, the schedules are averaged in order to get line frequencies.

  • link-based approach: in this approach, the assignment algorithm is not evaluating paths, or any aggregated information besides attributes stored by nodes and links. In the present case, each link has an associated cost (travel-time, \(s\)) and frequency (\(f = 1/s\)).

Elements of a transit network#

These are the elements required to describe an assignment graph.

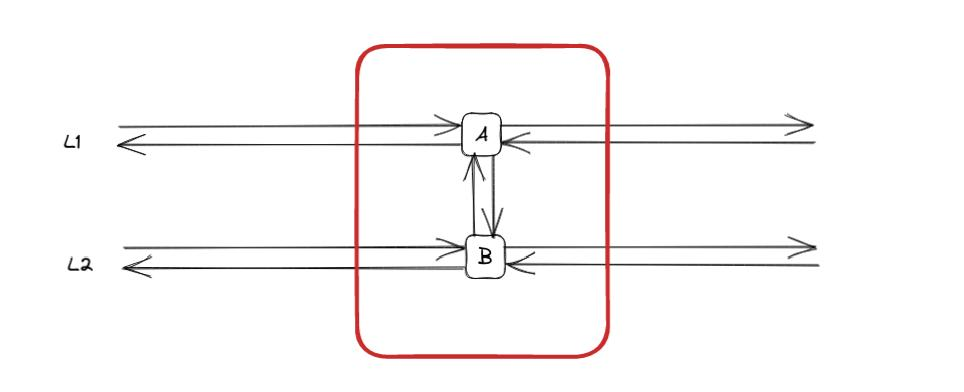
  • Transit stops and stations: transit stops are points where passenger can board, alight or change vehicles. Also, they can be part of larger stations. In the illustratation below, two distinct stops (‘A’ and ‘B’) are highlighted, and they are both affiliated with the same station (depicted in red).

    transit stops and stations

  • Transit lines: a transit line is a set of services that may use different routes, decomposed into segments.

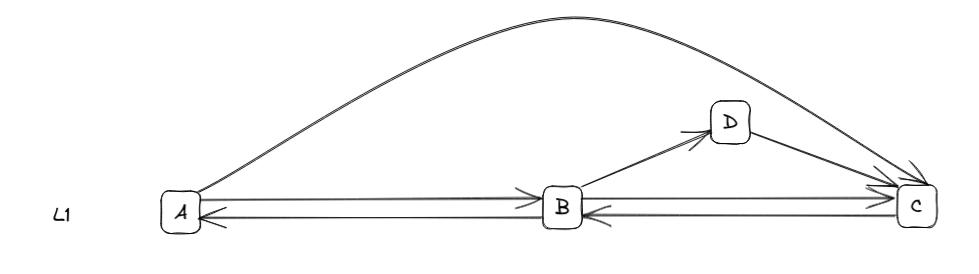
  • Transit routes: a route is described by a sequence of stop nodes. We assume here the routes to be directed. For example, we can take a simple case with 3 stops. In this case, the ‘L1’ line is made of two different routes: ‘ABC’ and ‘CBA’.

    transit routes 1

    A route can present various configurations, such as a partial route at a given moment of the day (‘AB’), a route with an additional stop (‘ABDC’), a route that does not stop at a given stop (‘AC’).

    transit routes 2

    Lines can also be decomposed into multiple sub-lines, each representing distinct routes. For the given example, we may have several sub-lines under the same commercial line (L1).

    Line ID

    Commercial Name

    Stop Sequence

    Headway (s)

    L1_a1

    L1

    ABC

    600

    L1_a2

    L1

    ABDC

    3,600

    L1_a3

    L1

    AB

    3,600

    L1_a4

    L1

    AC

    3,600

    L1_b1

    L1

    CBA

    600

    Associated with each sub-line, the headway corresponds to the mean time range between consecutive vehicles — the inverse of the line frequency used as a link attribute in the assignment algorithm.

  • Line segments: a line segment represents a portion of a transit line between two consecutive stops. Using the example line ‘L1_a1’, we derive two distinct line segments:

    Line ID

    Segment Index

    Origin Stop

    Destination Stop

    Travel Time

    L1_a1

    1

    A

    B

    300

    L1_a1

    2

    B

    C

    600

Note that a travel time is included for each line segment, serving as another link attribute used by the assignment algorithm.

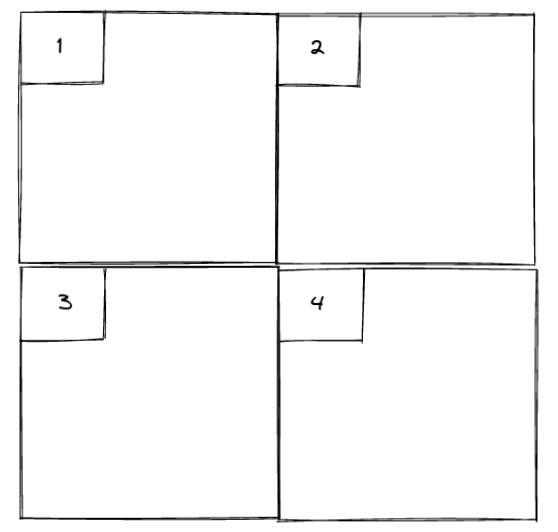
  • Transit Assignment Zones: transit assignment zones correspond to the partition of the network area. The illustration below presents 4 non-overlapping zones, whose demand is expressed as a number of trips from each zone to every other zone, forming a 4 x 4 Origin-Destination (OD) matrix.

    transit zones

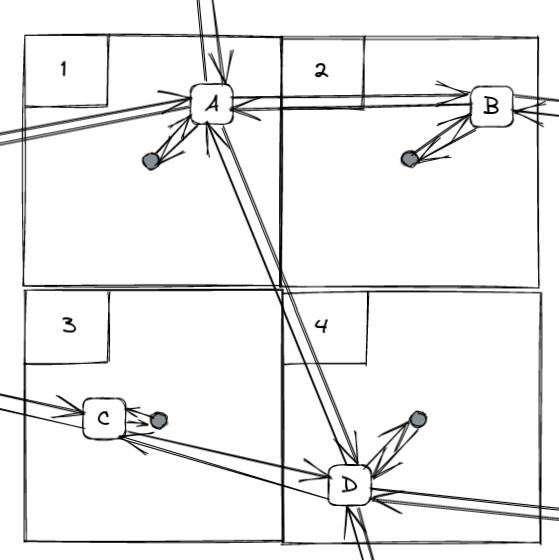
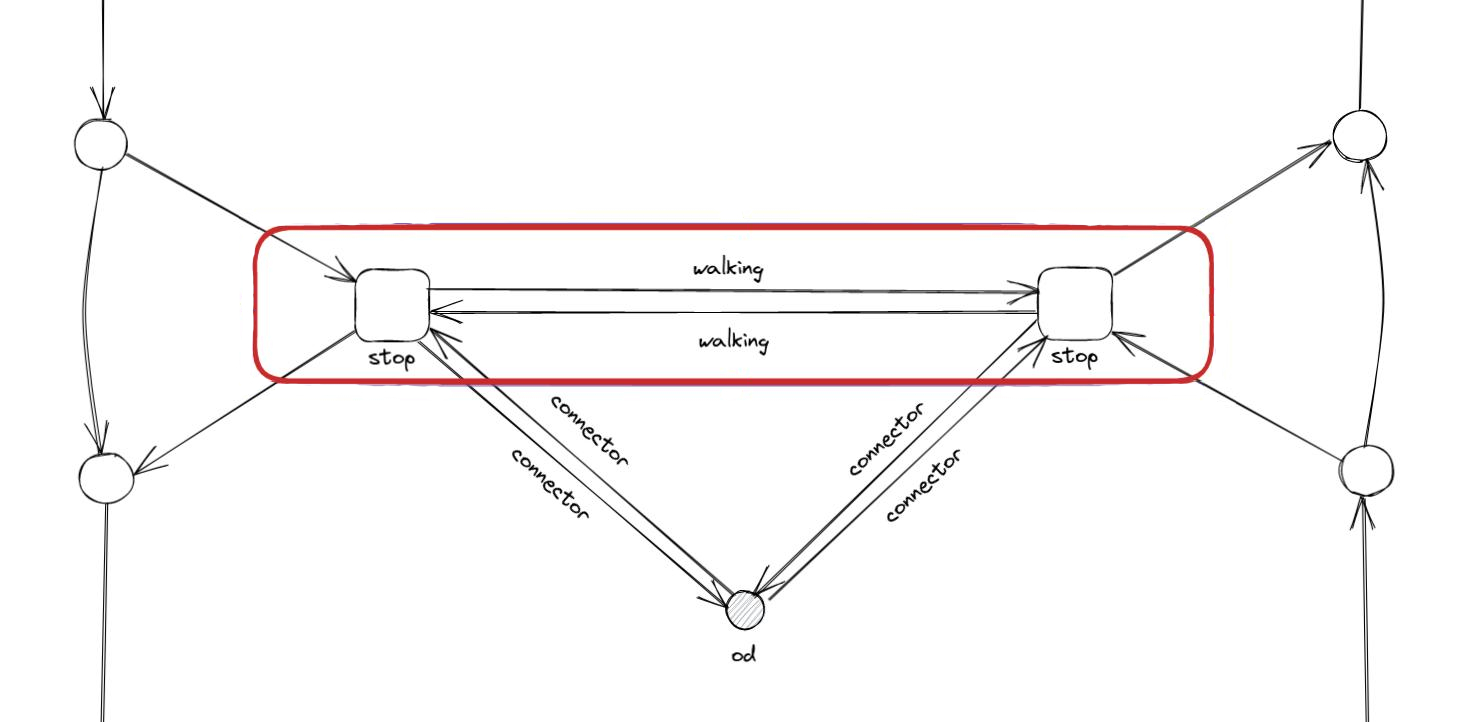
  • Connectors: connectors are special network nodes that facilitate the connection between supply and demand.

    transit connectors

The assignment graph#

The transit network is used to generate a graph with specific nodes and links used to model the transit process. Various link types and node categories play crucial roles in this representation.

Link types

Node types

On-board

Stop

Boarding

Boarding

Alighting

Alighting

Dwell

OD

Transfer

Walking

Connector

Walking

To illustrate, consider the anatomy of a simple stop (figure below). Waiting links encompass boarding and transfer links. Each line segment is associated with a boarding, an on-board and an alighting link.

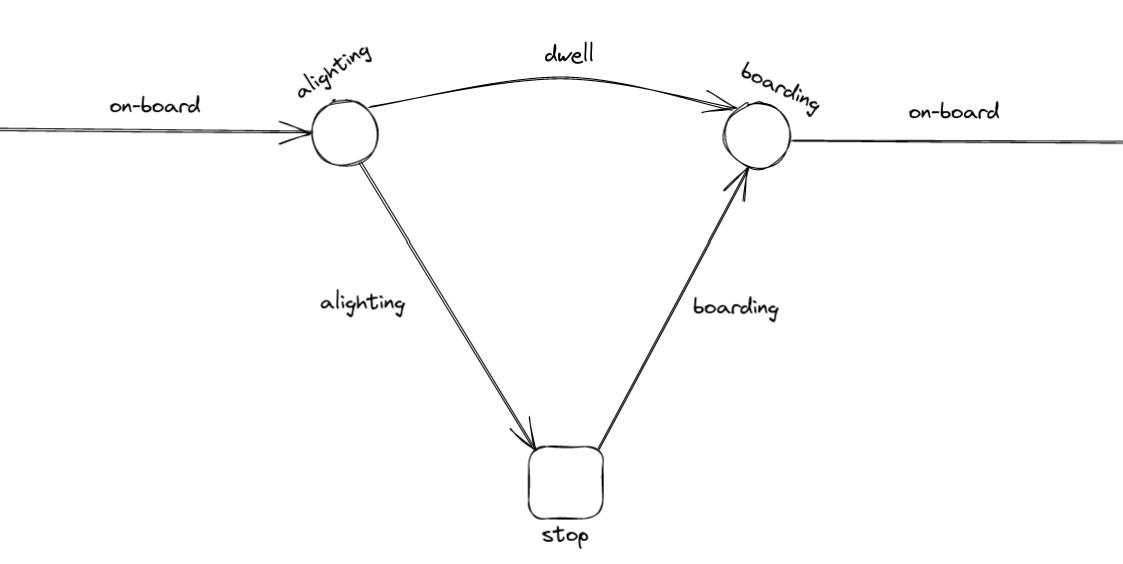
transit stop anatomy

Transfer links enable to compute the passenger flow count between line couples at the same stop. These links can be extended between all lines of a station if an increase in the number of links is viable.

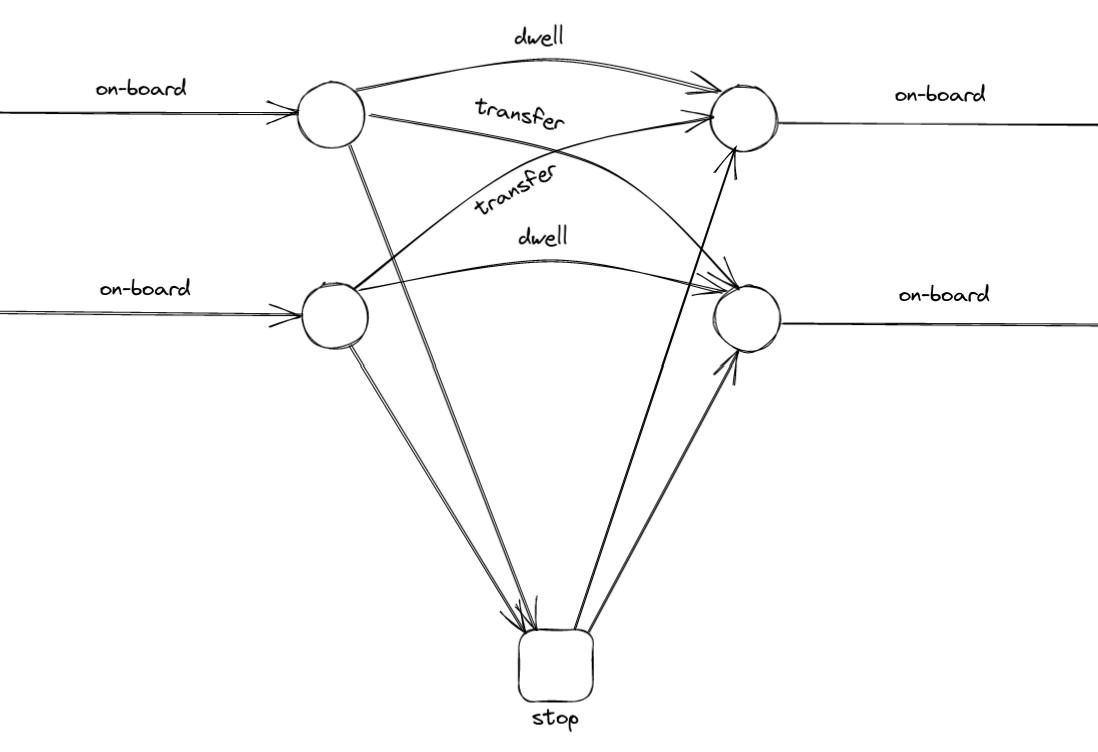
transfer links

Walking links connect stop nodes within a station, while connector links connect the zone centroids (OD nodes) to stop nodes. Connectors that connect OD to stop nodes allow passengers to access the network, while connectors in the opposite direction allow them to egress. Walking nodes/links may also be used to connect stops from distant stations.

walking links

The table below summarizes link characteristics and attributes based on link types:

Link Type

From node type

To node type

Cost

Frequency

on-board

boarding

alighting

travel time

\(\infty\)

boarding

stop

boarding

constant

line frequency

alighting

alighting

stop

constant

\(\infty\)

dwell

alighting

boarding

constant

\(\infty\)

transfer

alighting

boarding

constant + travel time

destination line frequency

connector

OD or stop

OD or stop

travel time

\(\infty\)

walking

stop or walking

stop or walking

travel time

\(\infty\)

The travel time is specific to each line segment or walking time. For example, there can be 10 minutes connection between stops in a large transit station. Constant boarding and alighting times are applied uniformly across the network, and dwell links have constant cost equal to the sum of the alighting and boarding constants.

Additional attributes can be introduced for specific link types, such as:

  • line_id: for on-board, boarding, alighting and dwell links.

  • line_seg_idx: the line segment index for boarding, on-board and alighting links.

  • stop_id: for alighting, dwell and boarding links. This can also apply to transfer links for inner stop transfers.

  • o_line_id: origin line ID for transfer links.

  • d_line_id: destination line ID for transfer links.

Assignment graph example - Based on Spiess and Florian (1989)#

This illustrative example is taken from Spiess and Florian (1989) [1].

The following figure presents the travel times for each line.

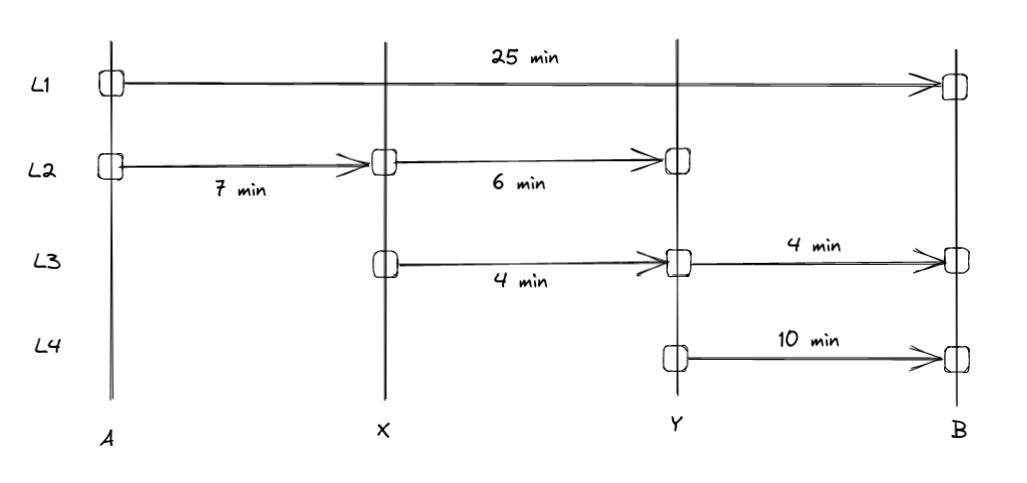
Spiess Florian 1

We have the following four distinct line characteristics:

Line ID

Route

Headway (min)

Frequency (1/s)

L1

AB

12

0.001388889

L2

AXY

12

0.001388889

L3

XYB

30

0.000555556

L4

YB

6

0.002777778

Passengers aim to travel from A to B, prompting the division of the network area into two distinct zones: TAZ 1 and TAZ 2. The assignment graph associated with this network encompasses 26 links:

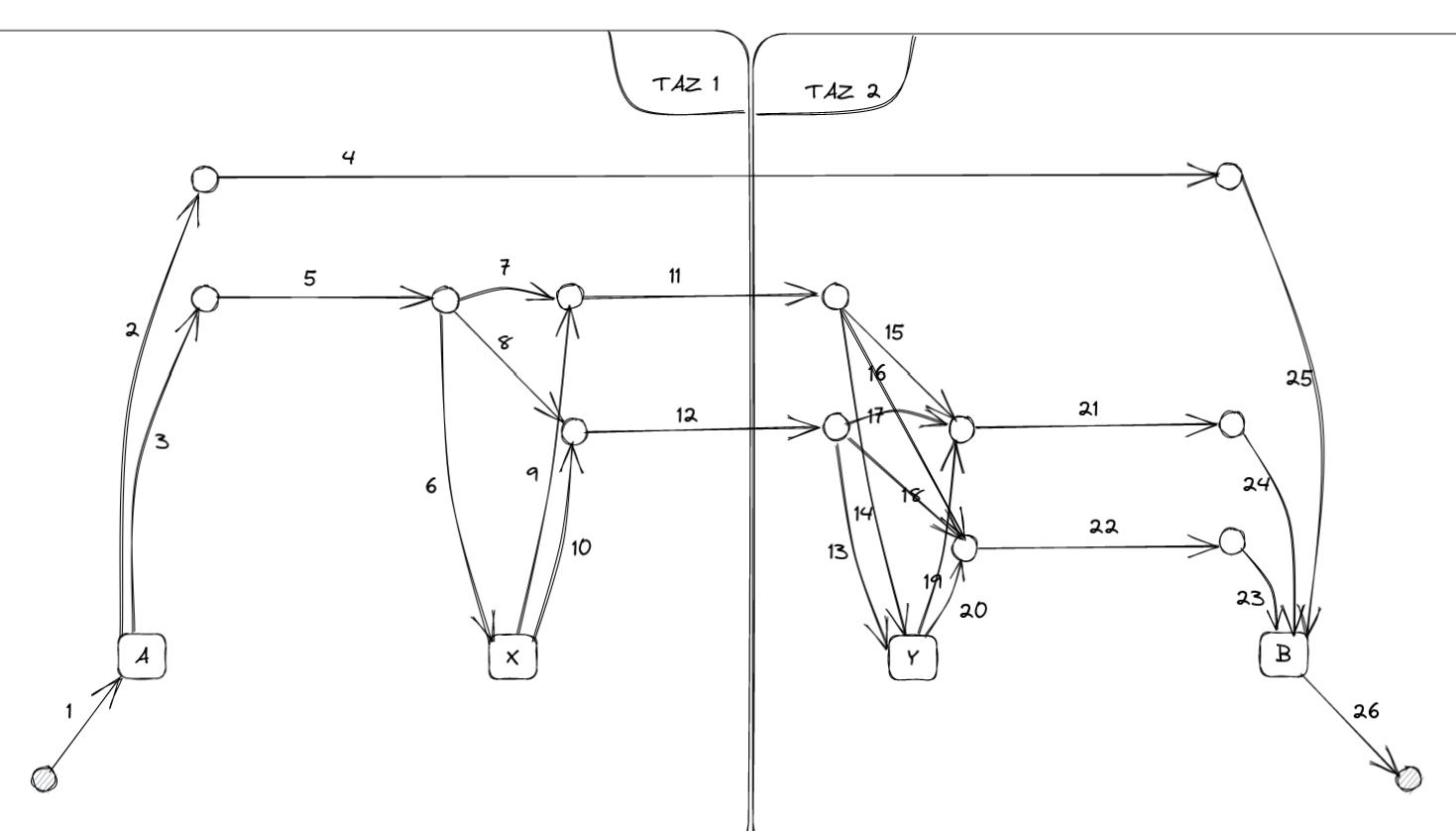
Spiess Florian 2

Here is a table listing all links:

Link ID

Link Type

Line ID

Cost

Frequency

1

connector

0

\(\infty\)

2

boarding

L1

0

0.001388889

3

boarding

L2

0

0.001388889

4

on-board

L1

1500

\(\infty\)

5

on-board

L2

420

\(\infty\)

6

alighting

L2

0

\(\infty\)

7

dwell

L2

0

\(\infty\)

8

transfer

0

0.000555556

9

boarding

L2

0

0.001388889

10

boarding

L3

0

0.000555556

11

on-board

L2

360

\(\infty\)

12

on-board

L3

240

\(\infty\)

13

alighting

L3

0

\(\infty\)

14

alighting

L2

0

\(\infty\)

15

transfer

L3

0

0.000555556

16

transfer

0

0.002777778

17

dwell

L3

0

\(\infty\)

18

transfer

0

0.002777778

19

boarding

L3

0

0.000555556

20

boarding

L4

0

0.002777778

21

on-board

L3

240

\(\infty\)

22

on-board

L4

600

\(\infty\)

23

alighting

L4

0

\(\infty\)

24

alighting

L3

0

\(\infty\)

25

alighting

L1

0

\(\infty\)

26

connector

0

\(\infty\)

Transit graph specificities in AequilibraE#

The graph creation process in AequilibraE incorporates several edge types to capture the nuances of transit networks. Notable distinctions include:

  • Connectors

    • access connectors: directed from od nodes to the network

    • egress connectors: directed from the network to the od nodes

  • Transfer edges

    • inner transfer: connect lines within the same stop

    • outer transfer: connect lines between distinct stops within the same station

  • Origin and destination nodes

    • origin nodes: represent the starting point of passenger trips

    • destination nodes: represent the end point of passenger trips

Users can customize these features using boolean parameters:

  • with_walking_edges: create walking edges between the stops of a station

  • with_inner_stop_transfers: create transfer edges between lines of a stop

  • with_outer_stop_transfers: create transfer edges between lines of different stops of a station

  • blocking_centroid_flow: duplicate OD nodes into unconnected origin and destination nodes in order to block centroid flows. Flows starts from an origin node and ends at a destination node. It is not possible to use an egress connector followed by an access connector in the middle of a trip.

Note that during the assignment, if passengers have the choice between a transfer edge or a walking edge for a line change, they will always be assigned to the transfer edge. This leads to these possible edge types:

  • on-board

  • boarding

  • alighting

  • dwell

  • access_connector

  • egress_connector

  • inner_transfer

  • outer_transfer

  • walking

References#