IPF Performance#
It is quite common to have zones with different growth rates. To improve obtaining a trip matrix, which satisfies both trip-end constraints, we can use iterative methods, such as the iterative proportional fitting (IPF). In this section, we compare the runtime of AquilibraE’s current implementation of IPF, with a general IPF algorithm, available here.
The figure below compares the AequilibraE’s IPF runtime with one core with the benchmark Python code. From the figure below, we can notice that the runtimes were practically the same for the instances with 1,000 zones or less. As the number of zones increases, AequilibraE demonstrated to be faster than the benchmark python code in instances with 1,000 < zones < 10,000, but it was a slower than the benchmark for the larger instances with 10,000 and 15,000 zones. It’s worth mentioning that the user can set up a threshold for AequilibraE’s IPF function, as well as use more than one core to speed up the fitting process.
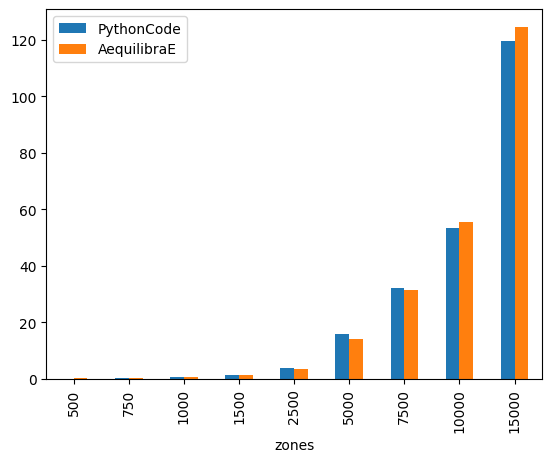
As IPF is an embarassingly-parallel workload, we have implemented our version in Cython, taking full advantage of parallelization and observing the impact of array orientation in memory. AequilibraE’s IPF allows the user to choose how many cores are used for IPF in order to speed up the fitting process, which is extremely useful when handling models with lots of traffic zones.
As we can see, instances with more zones benefited the most from the power of multi-processing speeding up the runtime in barely five times using five cores.
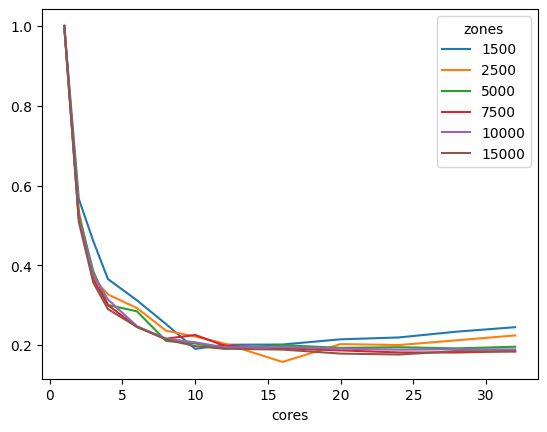
These tests were ran on a Threadripper 3970x (released in 2019) workstation with 32 cores (64 threads) @ 3.7 GHz and 256 Gb of RAM. With 32 cores in use, performing IPF took 0.105s on a 10,000 zones matrix, and 0.224 seconds on a 15,000 matrix. The code is provided below for convenience
# %%
from copy import deepcopy
from time import perf_counter
import numpy as np
import pandas as pd
from aequilibrae.distribution.ipf_core import ipf_core
from tqdm import tqdm
# %%
# From:
# https://github.com/joshchea/python-tdm/blob/master/scripts/CalcDistribution.py
def CalcFratar(ProdA, AttrA, Trips1, maxIter=10):
'''Calculates fratar trip distribution
ProdA = Production target as array
AttrA = Attraction target as array
Trips1 = Seed trip table for fratar
maxIter (optional) = maximum iterations, default is 10
Returns fratared trip table
'''
# print('Checking production, attraction balancing:')
sumP = ProdA.sum()
sumA = AttrA.sum()
# print('Production: ', sumP)
# print('Attraction: ', sumA)
if sumP != sumA:
# print('Productions and attractions do not balance, attractions will be scaled to productions!')
AttrA = AttrA*(sumP/sumA)
else:
pass
# print('Production, attraction balancing OK.')
# Run 2D balancing --->
for balIter in range(0, maxIter):
ComputedProductions = Trips1.sum(1)
ComputedProductions[ComputedProductions == 0] = 1
OrigFac = (ProdA/ComputedProductions)
Trips1 = Trips1*OrigFac[:, np.newaxis]
ComputedAttractions = Trips1.sum(0)
ComputedAttractions[ComputedAttractions == 0] = 1
DestFac = (AttrA/ComputedAttractions)
Trips1 = Trips1*DestFac
return Trips1
# %%
mat_sizes = [500, 750, 1000, 1500, 2500, 5000, 7500, 10000, 15000
cores_to_use = [1, 2, 3, 4, 6, 8, 10, 12, 16, 20, 24, 28, 32]
# %%
#Benchmarking
bench_data = []
cores = 1
repetitions = 3
iterations = 100
for zones in mat_sizes:
for repeat in tqdm(range(repetitions),f"Zone size: {zones}"):
mat1 = np.random.rand(zones, zones)
target_prod = np.random.rand(zones)
target_atra = np.random.rand(zones)
target_atra *= target_prod.sum()/target_atra.sum()
aeq_mat = deepcopy(mat1)
t = perf_counter()
# We use a nonsensical negative tolerance to force it to run all iterations
ipf_core(aeq_mat, target_prod, target_atra, max_iterations=iterations, tolerance=-5, cores=cores)
aeqt = perf_counter() - t
bc_mat = deepcopy(mat1)
t = perf_counter()
x = CalcFratar(target_prod, target_atra, bc_mat, maxIter=iterations)
bench_data.append([zones, perf_counter() - t, aeqt])
# %%
bench_df = pd.DataFrame(bench_data, columns=["zones", "PythonCode", "AequilibraE"])
bench_df.groupby(["zones"]).mean().plot.bar()
# %%
bench_df.groupby(["zones"]).mean()
# %%
#Benchmarking
aeq_data = []
repetitions = 1
iterations = 50
for zones in mat_sizes:
for cores in tqdm(cores_to_use,f"Zone size: {zones}"):
for repeat in range(repetitions):
mat1 = np.random.rand(zones, zones)
target_prod = np.random.rand(zones)
target_atra = np.random.rand(zones)
target_atra *= target_prod.sum()/target_atra.sum()
aeq_mat = deepcopy(mat1)
t = perf_counter()
ipf_core(aeq_mat, target_prod, target_atra, max_iterations=iterations, tolerance=-5, cores=cores)
aeqt = perf_counter() - t
aeq_data.append([zones, cores, aeqt])
# %%
aeq_df = pd.DataFrame(aeq_data, columns=["zones", "cores", "time"])
aeq_df = aeq_df[aeq_df.zones>1000]
aeq_df = aeq_df.groupby(["zones", "cores"]).mean().reset_index()
aeq_df = aeq_df.pivot_table(index="zones", columns="cores", values="time")
for cores in cores_to_use[::-1]:
aeq_df.loc[:, cores] /= aeq_df[1]
aeq_df.transpose().plot()