Note
Click here to download the full example code
7.12. Trip Distribution¶
On this example we calibrate a Synthetic Gravity Model that same model plus IPF (Fratar/Furness).
## Imports
from uuid import uuid4
from tempfile import gettempdir
from os.path import join
from aequilibrae.utils.create_example import create_example
import pandas as pd
import numpy as np
We create the example project inside our temp folder
fldr = join(gettempdir(), uuid4().hex)
project = create_example(fldr)
# We get the demand matrix directly from the project record
# so let's inspect what we have in the project
proj_matrices = project.matrices
proj_matrices.list()
# We get the demand matrix
demand = proj_matrices.get_matrix("demand_omx")
demand.computational_view(["matrix"])
# And the impedance
impedance = proj_matrices.get_matrix("skims")
impedance.computational_view(["time_final"])
Let’s have a function to plot the Trip Length Frequency Distribution
from math import log10, floor
import matplotlib.pyplot as plt
def plot_tlfd(demand, skim, name):
plt.clf()
b = floor(log10(skim.shape[0]) * 10)
n, bins, patches = plt.hist(
np.nan_to_num(skim.flatten(), 0),
bins=b,
weights=np.nan_to_num(demand.flatten()),
density=False,
facecolor="g",
alpha=0.75,
)
plt.xlabel("Trip length")
plt.ylabel("Probability")
plt.title("Trip-length frequency distribution")
plt.savefig(name, format="png")
return plt
from aequilibrae.distribution import GravityCalibration
for function in ["power", "expo"]:
gc = GravityCalibration(matrix=demand, impedance=impedance, function=function, nan_as_zero=True)
gc.calibrate()
model = gc.model
# we save the model
model.save(join(fldr, f"{function}_model.mod"))
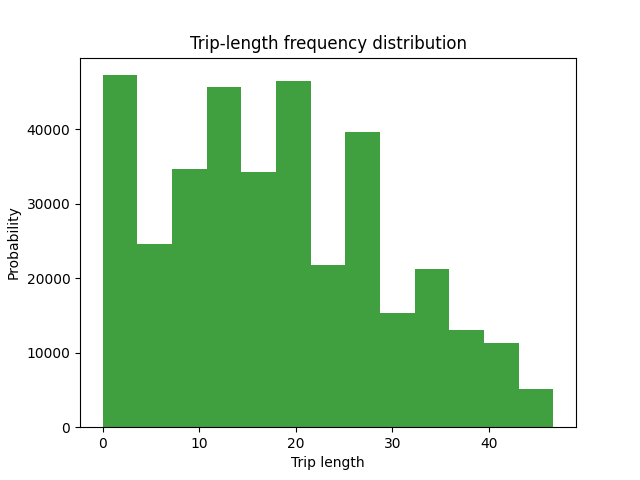
# We can save an image for the resulting model
_ = plot_tlfd(gc.result_matrix.matrix_view, impedance.matrix_view, join(fldr, f"{function}_tfld.png"))
# We can save the result of applying the model as well
# we can also save the calibration report
with open(join(fldr, f"{function}_convergence.log"), "w") as otp:
for r in gc.report:
otp.write(r + "\n")
Out:
/home/runner/work/aequilibrae/aequilibrae/aequilibrae/distribution/gravity_application.py:315: RuntimeWarning: divide by zero encountered in power
self.output.matrix_view[i, :] = (np.power(self.impedance.matrix_view[i, :], -self.model.alpha) * p
/home/runner/work/aequilibrae/aequilibrae/aequilibrae/distribution/gravity_application.py:326: RuntimeWarning: invalid value encountered in multiply
self.output.matrix_view[:, :] = self.output.matrix_view[:, :] * non_inf
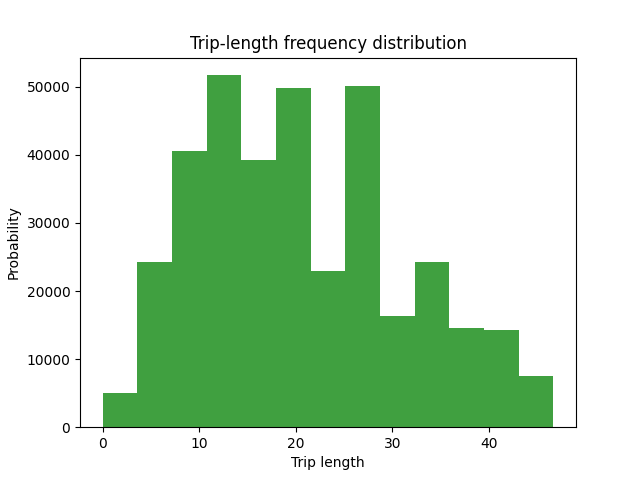
We save a trip length frequency distribution for the demand itself
plt = plot_tlfd(demand.matrix_view, impedance.matrix_view, join(fldr, "demand_tfld.png"))
plt.show()
## Forecast
# * We create a set of * 'future' * vectors by applying some models
# * We apply the model for both deterrence functions
from aequilibrae.distribution import Ipf, GravityApplication, SyntheticGravityModel
from aequilibrae.matrix import AequilibraeData
import numpy as np
zonal_data = pd.read_sql("Select zone_id, population, employment from zones order by zone_id", project.conn)
# We compute the vectors from our matrix
args = {
"file_path": join(fldr, "synthetic_future_vector.aed"),
"entries": demand.zones,
"field_names": ["origins", "destinations"],
"data_types": [np.float64, np.float64],
"memory_mode": True,
}
vectors = AequilibraeData()
vectors.create_empty(**args)
vectors.index[:] = zonal_data.zone_id[:]
# We apply a trivial regression-based model and balance the vectors
vectors.origins[:] = zonal_data.population[:] * 2.32
vectors.destinations[:] = zonal_data.employment[:] * 1.87
vectors.destinations *= vectors.origins.sum() / vectors.destinations.sum()
# We simply apply the models to the same impedance matrix now
for function in ["power", "expo"]:
model = SyntheticGravityModel()
model.load(join(fldr, f"{function}_model.mod"))
outmatrix = join(proj_matrices.fldr, f"demand_{function}_model.aem")
apply = GravityApplication()
args = {
"impedance": impedance,
"rows": vectors,
"row_field": "origins",
"model": model,
"columns": vectors,
"column_field": "destinations",
"nan_as_zero": True,
}
gravity = GravityApplication(**args)
gravity.apply()
# We get the output matrix and save it to OMX too,
gravity.save_to_project(name=f"demand_{function}_model_omx", file_name=f"demand_{function}_model.omx")
Out:
/home/runner/work/aequilibrae/aequilibrae/aequilibrae/distribution/gravity_application.py:315: RuntimeWarning: divide by zero encountered in power
self.output.matrix_view[i, :] = (np.power(self.impedance.matrix_view[i, :], -self.model.alpha) * p
/home/runner/work/aequilibrae/aequilibrae/aequilibrae/distribution/gravity_application.py:326: RuntimeWarning: invalid value encountered in multiply
self.output.matrix_view[:, :] = self.output.matrix_view[:, :] * non_inf
# We update the matrices table/records and verify that the new matrices are indeed there
proj_matrices.update_database()
proj_matrices.list()
### We now run IPF for the future vectors
args = {
"matrix": demand,
"rows": vectors,
"columns": vectors,
"column_field": "destinations",
"row_field": "origins",
"nan_as_zero": True,
}
ipf = Ipf(**args)
ipf.fit()
ipf.save_to_project(name="demand_ipf", file_name="demand_ipf.aem")
ipf.save_to_project(name="demand_ipf_omx", file_name="demand_ipf.omx")
Out:
<aequilibrae.project.data.matrix_record.MatrixRecord object at 0x7f0bec763850>
proj_matrices.list()
project.close()
Total running time of the script: ( 0 minutes 3.322 seconds)